Modul de rezistență
Acest articol va aborda importanța Modul de rezistență în societatea actuală. Modul de rezistență a câștigat relevanță în diferite domenii, de la modă la tehnologie, inclusiv cultură și politică. Influența sa s-a extins semnificativ în ultimii ani, generând un impact profund asupra modului în care oamenii interacționează și se relaționează unii cu alții. De aceea este esențial să analizăm în profunzime rolul pe care Modul de rezistență îl joacă în prezent, precum și posibilele sale implicații pe termen scurt și lung. În acest scop, diferite perspective și studii de caz vor fi examinate pentru a înțelege mai bine importanța și scopul Modul de rezistență în societatea contemporană.
În rezistența materialelor modulul de rezistență[1][2] este o proprietate geometrică a unei secțiuni transversale date utilizată la proiectarea grinzilor supuse la solicitări de încovoiere sau torsiune. Alte proprietăți geometrice utilizate în proiectare sunt aria secțiunii pentru tensiunile de întindere și forfecare, raza de inerție, momentul de inerție axial și cel polar pentru rigiditate. Orice relație între aceste proprietăți depinde în mare măsură de forma în cauză. Ecuațiile pentru modulele de rezistență ale formelor comune sunt date mai jos. Există două tipuri de module de rezistență, modulul de rezistență la încovoiere, Wz[3][4] și modulul de rezistență polar (la torsiune), Wp.[5][6] Modulele de rezistență ale diferitelor profile pot fi găsite și ca valori numerice pentru profile comune în tabelele care prezintă proprietățile acestora.[7]
Descriere
Modulul de rezistență la încovoiere față de axa x este dat de relația:[2]
unde este momentul de inerție axial al secțiunii față de axa x, iar este distanța până la axa x a celui mai îndepărtat punct al secțiunii.
Analog, pentru axa y momentul de rezistență la încovoiere este
Modulul de rezistență polar este dat de relația:[6]
unde este momentul de inerție polar față de centrul de greutate al secțiunii, iar este distanța până la centrul de greutate a celui mai îndepărtat punct al secțiunii.
Tabelul de mai jos prezintă formule pentru modulul de rezistență pentru diferite forme.[2][4][8]
| Forma secțiunii | Imagine | Relație | Note |
|---|---|---|---|
| Dreptunghi plin |

|
Săgeata plină reprezintă axa neutră | |
| Profil „I” axa principală |

|
, cu |
NA indică axa neutră |
| Profil „I” axa secundară |

|
[9] | NA indică axa neutră |
| Profil rotund | 
|
Săgeata plină reprezintă axa neutră | |
| Profil țeavă | 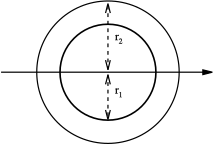
|
Săgeata plină reprezintă axa neutră | |
| Profil cheson | 
|
NA indică axa neutră | |
| Profil rombic plin |

|
NA indică axa neutră | |
| Profil „U” axa principală |
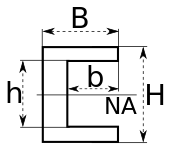
|
NA indică axa neutră |
Note
- ^ Andreescu, Mocanu, 2005, p. 115
- ^ a b c Hlușcu, Tripa, 2014, vol. I, pp. 105–108
- ^ Buzdugan, 1970, p. 119
- ^ a b Andreescu, Mocanu, 2005, p. 119
- ^ Buzdugan, 1970, p. 179
- ^ a b Hlușcu, Tripa, 2014, vol. II, p. 393
- ^ Buzdugan, 1970, Anexe
- ^ en Gere, J. M. and Timnko, S., 1997, Mechanics of Materials 4th Ed., PWS Publishing Co.
- ^ en „Section Modulus Equations and Calculators Common Shapes”.
Bibliografie
- Gheorghe Buzdugan, Rezistența materialelor, Ed. a IX-a revizuită, București: Editura Tehnică, 1970
- Indira Andreescu, Ștefan Mocanu, Compendiu de Rezistența Materialelor, (Universitatea Tehnică de Construcții din București), Editura Matrixrom, 2005, ISBN: 973-685-869-3
- Mihai Hlușcu, Pavel Tripa, Rezistența materialelor, Vol. I Arhivat în , la Wayback Machine. (curs Universitatea Politehnica Timișoara), Editura Mirton, 2014, ISBN: 978-973-521475-3
Vezi și
Legături externe
 Materiale media legate de modul de rezistență la Wikimedia Commons
Materiale media legate de modul de rezistență la Wikimedia Commons















