Dodecaedru parabiaugmentat
În lumea de astăzi, Dodecaedru parabiaugmentat a devenit un subiect de mare relevanță și interes pentru diverși oameni din întreaga lume. De la apariția sa, Dodecaedru parabiaugmentat a captat atenția experților și entuziaștilor deopotrivă, generând dezbateri aprofundate, cercetări și analize în jurul implicațiilor și repercusiunilor sale. Cu un impact palpabil asupra societății contemporane, Dodecaedru parabiaugmentat a reușit să pătrundă în diferite zone ale vieții cotidiene, de la politică la cultura populară, devenind un fenomen care nu lasă pe nimeni indiferent. În acest articol, vom explora în detaliu diferitele aspecte legate de Dodecaedru parabiaugmentat, evoluția sa în timp și influența sa asupra diferitelor aspecte ale societății actuale.
| Dodecaedru parabiaugmentat | |
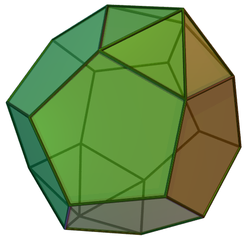 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J58 – J59 – J60 |
| Fețe | 20 (10 triunghiuri echilaterale 10 pentagoane)[1] |
| Laturi (muchii) | 40[1] |
| Vârfuri | 22[1] |
| χ | 2 |
| Configurația vârfului | 10 (53); 10 (32.52); 2 (35) |
| Grup de simetrie | D5d, , (2*5), ordin 20 |
| Arie | ≈ 21,535 a2 (a = latura) |
| Volum | ≈ 8,266 a3 (a = latura) |
| Poliedru dual | bitrunchi pentagonal giroalungit |
| Proprietăți | convex |
| Desfășurată | |
 | |
În geometrie dodecaedrul parabiaugmentat este un poliedru convex construit prin augmentarea unui dodecaedru prin atașarea a două piramide pentagonale (J2) la două din fețele sale opuse. Este poliedrul Johnson J59.[1][2] Când piramidele sunt atașate în ale moduri, rezultatul poate fi un dodecaedru augmentat (J58), un dodecaedru metabiaugmentat (J60), sau un dodecaedru triaugmentat (J61), iar dacă se admit și fețe neregulate, chiar și un dodecaedru pentakis. Având 20 de fețe, este un icosaedru, neregulat.
Mărimi asociate
Următoarele formule pentru arie, A și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Note
- ^ a b c d e en Stephen Wolfram, "Parabiaugmented dodecahedron" from Wolfram Alpha. Retrieved January 24, 2023.
- ^ en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603

