Figură izogonală
Aspect mută în bara laterală ascundeÎn geometrie, un politop (de exemplu un poligon, poliedru sau o pavare) este izogonal sau tranzitiv pe vârfuri dacă toate vârfurile sale sunt echivalente din punct de vedere al simetriilor sale. Aceasta implică faptul că fiecare vârf este înconjurat de aceleași tipuri de fețe, în aceeași ordine sau în ordine inversă, și cu aceleași unghiuri diedre între fețele corespunzătoare.
Din punct de vedere tehnic, se spune că pentru oricare două vârfuri există o simetrie a politopului care aplică unul dintre vârfuri izometric pe celălalt. Alte moduri de a spune acest lucru sunt că grupul de automorfisme al politopului acționează tranzitiv pe vârfuri sau că vârfurile se află într-o singură orbită de simetrie.
Toate vârfurile unei figuri izogonale finite n-dimensionale se află pe o (n−1)-sferă.
Termenul izogonal a fost folosit mult timp pentru poliedre. Tranzitiv pe vârfuri este un sinonim preluat de la noțiuni moderne ca grup de simetrie și teoria grafurilor.
Girobicupola pătrată alungită (pseudorombicuboctaedrul) — care nu este izogonală — demonstrează că simpla afirmație că „toate vârfurile arată la fel” nu este la fel de restrictivă ca definiția folosită aici, care implică grupul de izometrie care conservă poliedrul sau pavarea.
Poligoane și apeirogoane izogonale
| Apeirogoane izogonale |
|---|

|
| Apeirogoane nealiniate izogonale |
Toate poligoanele regulate, apeirogoanele și poligoanele stelate regulate sunt izogonale. Dualul unui poligon izogonal este un poligon izotoxal.
Unele poligoane cu un număr par de laturi și apeirogoane care au laturi alternante de două lungimi, de exemplu un dreptunghi, sunt izogonale.
Toate 2n-goanele plane izogonale au simetrie diedrală (Dn, n = 2, 3, ...) cu reflexia laturilor față de punctul lor din mijloc.
| D2 | D3 | D4 | D7 |
|---|---|---|---|
 Dreptunghiuri izogonale, simplu și autointersectate, având aceeași aranjare a vârfurilor |
 Haexagramă izogonală cu 6 vârfuri identice și 2 lungimi ale laturilor |
 Octogon convex izogonal cu axele de reflexie albastre și roșii |
 Tetradecagon „stelat” izogonal cu un tip de vârfuri și două tipuri de laturi |
Poliedre izogonale și pavări 2D
 Pavare pătrată deformată |
 Pavare pătrată trunchiată |
Un poliedru izogonal și pavările bidimensionale au un singur tip de vârf. Un poliedru izogonal cu toate fețele regulate este, de asemenea, un poliedru uniform și poate fi reprezentat printr-o notație de tip configurația vârfului cu ordinea fețelor din jurul fiecărui vârf. Variațiile deformate geometric ale poliedrelor și ale pavărilor uniforme pot fi și ele definite de configurația vârfului.
| D3d, ordinul 12 | Th, ordinul 24 | Oh, ordinul 48 | |
|---|---|---|---|
| 4.4.6 | 3.4.4.4 | 4.6.8 | 3.8.8 |
 prismă hexagonală deformată (trapezoprismă ditrigonală) |
 Rombicuboctaedru deformat |
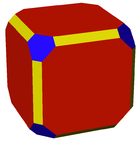 cuboctaedru puțin trunchiat |
 Cub hipertrunchiat |
Poliedrele izogonale și plăcile 2D pot fi clasificate după cum urmează:
- Regulate: sunt tranzitive pe vârfuri (izogonale), muchii (izoedrice) și fețe (izotoxale). (Asta implică faptul că toate fețele sunt poligoane regulate identice, și toate vârfurile sunt regulate.)
- Cvasiregulate: sunt tranzitive pe vârfuri și muchii (deci au fețe regulate) dar nu sunt tranzitive pe fețe. Dualul cvasiregulat este tranzitiv pe fețe și muchii (deci au vârfuri regulate) dar nu sunt tranzitive pe vârfuri.
- Semiregulate: sunt tranzitive pe vârfuri dar nu sunt tranzitive pe muchii, iar fețele sunt poligoane regulate. (Aceasta este una dintre definițiile noțiunii, în funcție de autor. Unele definiții se suprapun cu cele ale poliedrelor cvasiregulate.) Aceste poliedre includ prismele semiregulate și antiprismele. Dualul semiregulat este tranzitiv pe fețe dar nu este tranzitiv pe vârfuri, care însă sunt regulate.
- Uniforme: sunt tranzitive pe vârfuri și toate fețele sunt poligoane regulate, adică sunt regulate, cvasiregulate sau semiregulate. Dualul uniform dual este tranzitiv pe fețe și are vârfuri regulate, dar nu este necesar să fie tranzitiv și pe vârfuri.
- Semiuniforme: dacă elementele sale sunt și izogonale.
- Scaliforme: dacă toate laturile au aceeași lungime.
- Nobile: sunt tranzitive pe fețe și vârfuri dar nu în mod necesar și pe muchii. Poliedrele regulate sunt și nobile; singurele poliedre uniforme nobile. Dualele poliedrelor nobile sunt și ele nobile.
Aceste definiții pot fi extinse la politopuri din dimensiuni superioare și la teselări. Toate politopurile uniforme sunt izogonale, de exemplu, 4-politopurile uniforme și fagurii uniformi convecși.
Dualul unui politop izogonal este o figură izoedrică, care este tranzitivă pe fațete.
Figuri k-izogonale și k-uniforme
Un politop sau o pavare pot fi numite „k-izogonale” dacă vârfurile sale formează clase de tranzitivitate k. Un termen mai restrictiv, „k-uniform” este definit ca o figură k-izogonală construită numai din poligoane regulate. Ele pot fi reprezentate vizual prin colorarea uniformă cu diverse culori.
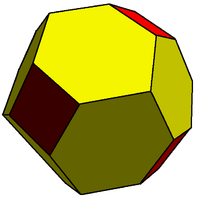 Acest dodecaedru rombic trunchiat este 2-izogonal deoarece conține două clase de tranzitivitate a vârfurilor. Acest poliedru este format din pătrate și hexagoane. |
 Această pavare semiregulată este, de asemenea, 2-izogonală (și 2-uniformă). Această pavare este formată din triunghiuri și hexagoane regulate. |
 Eneagramă 9/4 2-izogonală (fața icosaedrului stelat final) |
Note
- ^ en Coxeter, The Densities of the Regular Polytopes II, p54-55, "hexagram" vertex figure of h{5/2,5}.
- ^ en Branko Grünbaum, The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Figure 1. Parameter t=2.0
Bibliografie
- en Peter R. Cromwell, Polyhedra, Cambridge University Press 1997, ISBN: 0-521-55432-2, p. 369 Transitivity
- en Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns
 . W. H. Freeman and Company. ISBN 0-7167-1193-1. (p. 33 k-isogonal tiling, p. 65 k-uniform tilings)
. W. H. Freeman and Company. ISBN 0-7167-1193-1. (p. 33 k-isogonal tiling, p. 65 k-uniform tilings)
Legături externe
- en Eric W. Weisstein, Vertex-transitive graph la MathWorld.
- en George Olshevsky. „Transitivity”. Glossary for Hyperspace. Arhivat din original la 4 februarie 2007.
- en George Olshevsky. „Isogonal”. Glossary for Hyperspace. Arhivat din original la 4 februarie 2007.
- en Isogonal Kaleidoscopical Polyhedra Vladimir L. Bulatov, Physics Department, Oregon State University, Corvallis, Presented at Mosaic2000, Millennial Open Symposium on the Arts and Interdisciplinary Computing, 21–24 August 2000, Seattle, WA VRML models
- en Steven Dutch uses the term k-uniform for enumerating k-isogonal tilings
- en List of n-uniform tilings
- en Eric W. Weisstein, Demiregular tessellations la MathWorld. (Folosește termenul „k-uniform” pentru „k-izogonal”)