Poligon stelat

În lumea Poligon stelat, există o mulțime de informații și opinii care pot fi copleșitoare pentru cei care doresc să înțeleagă mai bine acest subiect. Din diferite perspective și abordări, Poligon stelat a fost subiect de dezbatere și discuție de-a lungul istoriei, iar relevanța sa în societatea actuală continuă să fie un subiect de mare interes. În acest articol, vom explora multiplele fațete ale Poligon stelat, cu scopul de a oferi o viziune completă și îmbogățitoare a acestui subiect foarte relevant. De la originea și până la impactul său astăzi, ne vom porni într-o călătorie de descoperire pentru a înțelege mai bine Poligon stelat și relația sa cu lumea din jurul nostru.

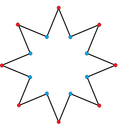
Nu confundați cu Poligon în formă de stea.
Două tipuri de pentagoane stelate

{5/2}
|5/2|
Pentagonul regulat, {5/2}, are cinci vârfuri și laturi care se intersectează, în timp ce decagonul concav, |5/2|, are zece laturi și două mulțimi de cinci vârfuri. Primul este folosit la definirea poliedrelor stelate și ale pavărilor uniforme cu plăci stelate, în timp ce al doilea este uneori utilizat în pavările plane.

Micul dodecaedru stelat
Teselare

În geometrie, un poligon stelat este un tip de poligon neconvex. Numai poligoanele stelate regulate au fost studiate în profunzime.

Poligoanele stelate par să nu fi fost definite formal. Unele pot apărea prin operații de trunchiere a poligoanelor simple și stelate regulate. Branko Grünbaum a identificat două definiții primare utilizate de Johannes Kepler, prima fiind cea a poligonelor stelate regulate cu laturi care se intersectează fără a genera noi vârfuri, iar al doua fiind a poligoanelor concave izotoxale.[1]

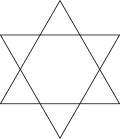
Prima se referă la poligrame, care sunt poligoane precum pentagrama, dar și figuri compuse precum hexagrama.

Etimologie

Numele poligoanelor stelate combină un prefix numeric, cum ar fi penta-, cu sufixul grecesc -gram (în acest caz generând cuvântul pentagramă). Prefixul este în mod normal un număr cardinal grec, dar există sinonime care folosesc alte prefixe. De exemplu, un poligon cu nouă colțuri sau eneagramă este de asemenea cunoscut sub numele de nonagramă, folosind prefixul ordinal latin nona-. Sufixul -gramă vine din greacă γραμμή (română linie).[2]

Poligoane stelate regulate

Poligoane convexe și stelate regulate cu 3 până la 12 vârfuri etichetate cu simbolurile lor Schläfli

Un "poligon stelat regulat" este un poligon echilateral, echiunghiular a cărui laturi se intersectează. Simbolurile lor Schläfli sunt de forma {p/q}, unde p (numărul vârfurilor) și q (pasul stelării) sunt coprime (nu au divizori comuni) iar q ≥ 2.

Grupul de simetrie al {n/k} este un grup diedral Dn de ordinul 2n, independent de k.

Poligoanele stelate regulate au fost studiate sistematic pentru prima oară de Thomas Bradwardine, iar apoi de Johannes Kepler.[3]

Construcția prin conectarea vârfurilor

Poligoanele stelate regulate pot fi create prin conectarea unui vârf dintr-un poligon regulat, simplu, cu p-laturi cu un alt vârf neadiacent și continuarea procesului cu același pas între vârfuri până ce se ajunge din nou în vârful inițial.[4] Alternativ, pentru numerele întregi p și q, acesta poate fi construit prin conectarea fiecărui al „q”-lea vârf dintre punctele „p” distanțate în mod regulat pe un cerc.[5] De exemplu, un pentagon regulat (o stea cu cinci colțuri) poate fi obținut trasând o linie de la primul la al treilea vârf, de la al treilea vârf la al cincilea, de la al cincilea la al doilea, de la al doilea la al patrulea și de la al patrulea la primul vârf.

Dacă q este mai mare decât jumătate din p, atunci construcția va avea ca rezultat același poligon ca și p-q; conectarea fiecărui al treilea vârf al pentagonului va produce un rezultat identic cu cel al conectării fiecărui al doilea vârf. Însă vârfurile vor fi atinse în ordine inversă, ceea ce contează atunci când poligoanele retrograde sunt încorporate în politopuri de dimensiuni superioare. De exemplu, o antiprismă formată dintr-o pentagramă {5/2} are ca rezultat o antiprismă pentagramică; construcția analogă dintr-o pentagramă retrogradă {5/3} are ca rezultat o retroprismă pentagramică. Un alt exemplu este tetrahemihexahedrul, care poate fi văzut ca o cupolă {3/2}.

Poligoane stelate regulate degenerate

Hexagon degenerat

Dacă p și q nu sunt coprime va rezulta un poligon degenerat cu vârfuri și laturi care coincid. De exemplu {6/2} va apărea ca un triunghi, dar poate fi etichetat cu două mulțimi de vârfuri: (1, 2, 3) și (4, 5, 6). Acest lucru ar trebui văzut nu ca două triunghiuri suprapuse, ci o dublă înfășurare a unui singur hexagon.[6][7]

Construcția prin stelare

Alternativ, un poligon stelat regulat poate fi obținut și ca o secvență de stelare a „corpului” unui poligon regulat convex. Construcțiile bazate pe stelare permit, de asemenea, obținerea compușilor poligonali regulați în cazurile în care numărul și pasul vârfurilor nu sunt coprime. Însă atunci când de construiesc poligoane stelate prin stelare, dacă q este mai mare decât p/2, liniile vor fi divergente, iar dacă q este egal cu p/2 liniile vor fi paralele, în ambele cazuri neapărând vreo altă intersecție în spațiul euclidian. Totuși, astfel de poligoane pot fi construite în spațiul sferic, similar cu monogonul și digonul. (Astfel de poligoane nu par să fi fost încă studiate în detaliu.)

Poligoane în formă de stea

Când segmentele interioare rezultate din intersecții sunt îndepărtate, poligoanele stelate nu mai sunt regulate, dar pot fi privite ca poligoane în formă de stea adică ] concave izotoxale 2n-gonale, cu vârfurile alternând pe două cercuri cu raze diferite și care nu trebuie să se potrivească neapărat cu unghiurile poligonului stelat regulat. Branko Grünbaum în Tilings and Patterns (română Pavări și Modele) notează aceste stele — |n/d|, care notație se potriveșye cu geometria poligramelor {n/d} — cu o notație {nα} mai generală, reprezentând o stea cu n laturi cu fiecare unghi intern α <  (1 – 2/n)‧180°.[1] Pentru |n/d|, vârfurile interioare au unghiul exterior, β, de (d – 1)/n‧360°.

Exemple de poligoane stea simple izotoxale
|n/d|
{nα} 		 
{330°} 		 
{630°} 		|5/2|
{536°} 		 
{445°} 		|8/3|
{845°} 		|6/2|
{660°} 		 
{572°}
α 30° 36° 45° 60° 72°
β 150° 90° 72° 135° 90° 120° 144°
Stele
izotoxale
Poligrame
asociate
 
{n/d}
 
{12/5}
{5/2}
{8/3}
2{3}
Stea
{10/3}

Exemple de pavări

Aceste poligoane apar adesea în modelele de pavări. Unghiul parametric α (grade sau radiani) poate fi ales pentru a se potrivi cu unghiurile interne ale poligoanelor vecine într-un model de teselare. Johannes Kepler în lucrarea sa din 1619 Harmonices Mundi a inclus între altele pavările periodice și neperiodice precum cele cu trei pentagone regulate și un pentagon stelat regulat (5.5.5.5/2) care se potrivesc în jurul un vârf, înrudite cu modernele pavări Penrose.[8]

Exemple de pavări cu poligoane stea izotoxale[9]
Stele triunghiulare Stele pătrate Stele hexagonale Stele octogonale

(3.3*
α.3.3**
α)
(8.4*
π/4.8.4*
π/4)
(6.6*
π/3.6.6*
π/3)
(3.6*
π/3.6**
π/3)
(3.6.6*
π/3.6)
Not edge-to-edge

Interiorul poligoanelor stelate

Interiorul unui poligon stelat poate fi tratat în moduri diferite. În imaginea de alături sunt ilustrate trei astfel de tratări pentru o pentagramă. Branko Grünbaum și Geoffrey Shephard consideră două dintre ele ca fiind 2n-poligoane stelate regulate concave izogonale.[8]

Cele trei tratări sunt:

  • La fiecare latură o parte este tratată ca fiind în exterior și cealaltă parte ca fiind în interior. Acest lucru este prezentat în imaginea din stânga și apare frecvent în grafica vectorială computerizată.
  • Numărul de câte ori curba poligonală se înfășoară în jurul unei anumite regiuni reprezintă densitatea. Exteriorul are densitatea 0 și orice regiune cu densitate > 0 este considerată ca fiind interioară. Acest lucru este prezentat în imaginea din mijloc și apare frecvent la prelucrarea matematică a poliedrelor. (Totuși, la poliedrele neorientabile densitatea trebuie considerată doar modulo 2, prin urmare primul tratament este uneori folosit în aceste cazuri pentru consistență.)
  • Zona în care orice punct din interior poate fi legat cu un alt punct din interior printr-un segment care nu intersectează frontiera este tratată ca fiind interiorul figurii. Acest lucru este prezentat în imaginea din dreapta și apare frecvent atunci când se realizează un model fizic.

La calculul ariei poligonului fiecare dintre aceste abordări dă un altă valoare.

Note

  1. ^ a b Grünbaum & Shephard 1987, section 2.5.
  2. ^ en γραμμή, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
  3. ^ en Coxeter, Introduction to Geometry, second edition, 2.8 Star polygons pp. 36–38
  4. ^ en Coxeter, Harold Scott Macdonald (). Regular polytopes. Courier Dover Publications. p. 93. ISBN 978-0-486-61480-9. 
  5. ^ en Eric W. Weisstein, Star Polygon la MathWorld.
  6. ^ en Branko Grünbaum, Are Your Polyhedra the Same as My Polyhedra? Arhivat în , la Wayback Machine., math.washington.edu, accesat 2021-02-09
  7. ^ en Coxeter, The Densities of the Regular polytopes I, p.43: If d is odd, the truncation of the polygon {p/q} is naturally {2n/d}. But if not, it consistents of two coincident {n/(d/2)}'s; two, because each side arises from an original side and once from an original vertex. Thus the density of a polygon is unaltered by truncation.
  8. ^ a b en Branko Grunbaum and Geoffrey C. Shephard, Tilings by Regular Polygons Arhivat în , la Wayback Machine., Mathematics Magazine 50 (1977), 227–247 and 51 (1978), 205–206]
  9. ^ en Joseph Myers, Tiling with Regular Star Polygons, polyomino.org.uk, accesat 2021-02-09

Bibliografie

  • en Grünbaum, B., G.C. Shephard; Tilings and Patterns, New York: W. H. Freeman & Co., (1987), ISBN: 0-7167-1193-1
  • en Grünbaum, B., Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993), ed T. Bisztriczky et al., Kluwer Academic (1994) pp. 43–70
  • en Grünbaum, B., Metamorphoses of polygons, published in The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994)
  • en Cromwell, P.; Polyhedra, CUP, Hbk. 1997, ISBN: 0-521-66432-2. Pbk. (1999), ISBN: 0-521-66405-5, p. 175
  • en John Horton Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)

Legături externe

Portal icon Portal matematică