Radian
În zilele noastre, Radian este un subiect care se află în centrul atenției și al dezbaterii în diferite domenii. Implicațiile și repercusiunile sale sunt de mare importanță, așa că este esențial să o analizăm din diverse perspective. În acest articol, vom explora diferite aspecte legate de Radian, examinând impactul acestuia asupra societății, evoluția sa în timp și posibilele soluții sau abordări care pot fi luate în considerare. Acest subiect este de interes general și relevanța sa nu poate fi ignorată, așa că este esențial să-l înțelegem în mod cuprinzător pentru a lua decizii în cunoștință de cauză și pentru a promova un dialog constructiv despre el.
| Acest articol sau această secțiune are bibliografia incompletă sau inexistentă. Puteți contribui prin adăugarea de referințe în vederea susținerii bibliografice a afirmațiilor pe care le conține. |
| Radian | |
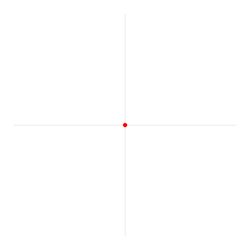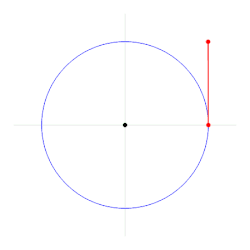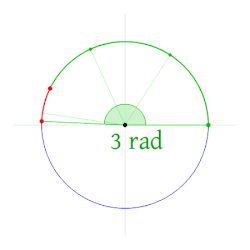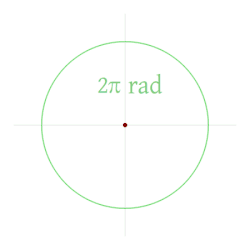 Un arc de cerc egal in lungime cu raza cercului corespunde unui unghi de 1 radian. Un cerc corespunde unui unghi de 2π radian. | |
| Nume | radian |
|---|---|
| Mărime | Distanță unghiulară[1][2] |
| Unitatea în SI | 1 radian |
| Modifică date / text | |
Un radian, având simbolul rad, este o unitate de măsură pentru măsura unghiurilor. Este unghiul care, având vârful în centrul unui cerc, intersectează pe circumferința acestuia un arc a cărui lungime este egală cu lungimea razei cercului. Măsura în radiani a unui unghi la centru este numeric egală cu lungimea arcului de cerc unitate (cu raza 1) corespunzător.
Un radian este egal 180°/π sau aproximativ 57,2958° sau 57°17'45.
Lungimea unui arc de cerc este egală cu raza înmulțită cu măsura în radiani a arcului.
Radianul face parte din Sistemul Internațional.
În matematică, unghiurile se exprimă de obicei în radiani, fără a scrie însă unitatea de măsură.

Transformarea dintre radiani și grade

Un radian este egal cu 180°/π. Pentru a transforma din radiani în grade, numărul radianilor se înmulțește cu 180/π. De exemplu:
Invers, pentru a transforma din grade în radiani, numărul gradelor se înmulțește cu π/180. De exemplu:
Istoric
Conceptul de radian ca unitate de măsură e atribuit de obicei lui Roger Cotes. Era cunoscut și matematicienilor arabo-persani ca de exemplu Al-Kashi.
Avantajele pentru a măsura în radiani
| Calitatea informațiilor sau a exprimării din acest articol sau secțiune trebuie îmbunătățită. Consultați manualul de stil și îndrumarul, apoi dați o mână de ajutor. |

În calcule și cele mai multe alte ramuri ale matematicii dincolo de geometrie practică, unghiurile sunt universal măsurate în radiani. Acest lucru se datorează faptului că radianii au o "naturalețe" matematică, care conduce la o formulare mai elegantă a unui număr de rezultate importante.
Statut dimensional
Este o unitate de măsură pentru o mărime adimensională deoarece este definit ca raport a două lungimi.
Vezi și
- Miliradian sau miime
Note
- ^ SI A concise summary of the International System of Units, SI (PDF)
- ^ 6.5.3, Quantities and units—Part 1: General, p. 18





